Fraktale
Sie sind in uns, auf uns und sie umgeben uns in vielfältigen Formen in der Natur. Man kann sie mithilfe mathematischer Formeln beschreiben, für die Wettervorhersage ebenso nutzen, wie für die Verbesserung von technischen Bauteilen. Und seit dem Computer leistungsfähig genug sind, um in annehmbarer Zeit grafische Darstellungen dieser mathematischen Formeln zu berechnen, kann man sich diese Grafiken als Kunstwerk an die Wand hängen: Fraktale.
Fraktale sind komplexe geometrische Muster natürlichen oder künstlichen Ursprungs, die Selbstähnlichkeit aufweisen. Das ist beispielsweise der Fall, wenn ein Objekt aus mehreren verkleinerten Kopien seiner selbst besteht. Geprägt wurde der Begriff Fraktale von dem bedeutendsten Wissenschaftler auf dem Gebiet der fraktalen Geometrie, Benoit Mandelbrot. Er nutzte die fraktale Geometrie um in der Natur vorkommende komplexe Strukturen zu beschreiben, die mit der klassischen Geometrie nicht zu beschreiben sind und mathematische Fragestellungen zu lösen, wie die Länge der Küstenlinie einer Insel oder die Größe der Oberfläche eines Gebirges. Schnell wurde klar, dass sich mit der fraktalen Geometrie auch Bilder erzeugen lassen, die ästhetisch ansprechend sind. Die komplexen Strukturen der Fraktale mit ihrem ungeheuren Formenreichtum und ihrer eigenwilligen Schönheit haben selbst Menschen in ihren Bann gezogen, die sonst lieber einen großen Bogen um die Mathematik machen.
Erzeugen lassen sich Fraktal-Bilder entweder grafisch, durch wiederholen eines einfachen Musters, oder mathematisch.
Grafische Erzeugung von Fraktalbildern
Die grafische Erzeugung von Fraktalbildern beruht auf der Methode, ein einfaches Muster mit einer einfachen Anweisungen zur Wiederholung des Muster zu kombinieren. Auf diese Weise lassen sich ohne irgendwelche Mathematikkenntnisse Fraktale erzeugen. Das kann man am Beispiel der, nach dem deutschen Mathematiker Helge von Koch benannten, Koch'schen Schneeflocke erkennen. Man nimmt ein gleichseitiges Dreieck und ersetzt die Seiten durch _/\_. Anschließend wiederholt man den Vorgang mit den neu entstandenen Seiten und einem, der neuen Länge der Seiten angepassten _/\_. Bereits nach wenigen Wiederholungen, Iterationen genannt, entsteht eine komplexe Struktur, die an eine Schneeflocke erinnert.
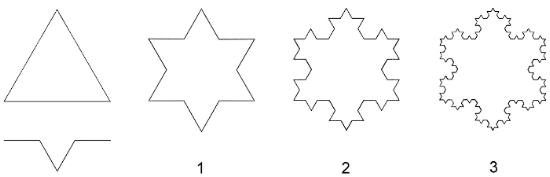
Koch'sche Schneeflocke
Aus dieser Vorgehensweise ergibt sich eine wesentliche Eigenschaft von Fraktalen: Die Selbstähnlichkeit. Ein kleiner Teil des fraktalen Musters ähnelt sehr stark dem gesamten Muster. Oder andersherum gesagt: Das Muster besteht aus verkleinerten Kopien seinerselbst.
Weiterhin ist erkennbar, dass die Länge der Linie der Koch'schen Schneeflocke mit jedem Iterationsschritt zunimmt. Würde man unendlich viele Iterationen durchführen, wäre die Linie unendlich lang. Damit ist auch die Frage nach der Länge der Küstenlinie einer Insel beantwortet. Zwar ist die Selbstähnlichkeit nicht so offensichtlich ausgeprägt, dennoch ist auch sie unendlich, wenn man keinen Maßstab angibt, der eine Untergrenze der Feinheiten der Struktur vorgibt.
Ein weiteres Beispiel ist das Sierpinski-Dreieck, benannt nach dem polnischen Mathematiker Waclav Sierpinski. Man zeichnet ein gleichseitiges Dreieck und verbindet die Mittelpunkte der Seiten miteinander zu einem neuen Dreieck und entfernt dieses, wodurch die Figur nun aus drei kleineren Dreiecken besteht. Dann wiederholt man den Vorgang mit diesen Dreiecken. Auch hier erhält man nach wenigen Iterationen ein komplexes Gebilde. Von dem Dreieck bleibt nicht mehr viel übrig, während die Länge der Linie zunimmt. Nach unendlich vielen Iterationen umschließt eine unendlich lange Linie (Dimension 1) eine Fläche (Dimension 2) von fast 0. Das Sierpinski-Dreieck besitzt deshalb eine Dimension zwischen eins und zwei. Daran zeigt sich eine weitere Eigenschaft von Fraktalen: die gebrochene Dimension. Daher auch die Bezeichnung Fraktal, von Latein fractus = gebrochen, zerbrochen. Das Sierpinski-Dreieck besitzt eine Dimension von ca. 1,89.

Sierpinski-Dreieck
Mathematische Erzeugung von Fraktalbildern
Bei der mathematische Erzeugung von Fraktalbildern handelt es sich um grafische Darstellungen bestimmter Eigenschaften von mathematischen Formeln. Das komplizierte daran sind aber weniger die Formeln, sondern vielmehr das mathematische Verfahren und die notwendigen Berechnungen. Das mathematische Verfahren ist um einiges komplizierter als eine Kurvendiskussion, an die sich der eine oder andere vielleicht noch aus der Schulzeit erinnert. Und der Rechenaufwand ist so riesig, dass es ohne Computer kaum möglich ist diese Bilder zu erzeugen. Ein Mensch würde oft Jahre, mitunter sogar länger als ein Menschenleben benötigen. Auch die ersten Computer brauchten sehr lange für die Berechnung. Als in den 1980ern die ersten PC's Einzug in die Privathaushalte erhielten, und mit speziellen Programmen die Berechnung von Fraktalbildern ermöglichten, hieß es oft tagelang: Bloß nicht Maus und Tastatur anfassen, sonst stürzt das Programm vielleicht ab und alles war umsonst. Und die berechneten Bilder hatten meist nicht einmal eine Auflösung von 640 x 480 Pixeln. Heute benötigen normale PC's deutlich weniger als eine Minute für ein derartiges Bild, selbst für die Berechnung von Bildern in Postergröße werden nur wenige Minuten benötigt. Länger dauert es bei den 3D-Fraktalen.
Anhand eines Beispiels aus der Biologie soll das mathematische Verfahren teilweise erklärt werden:
Zoologen erforschen das Leben bestimmter Tierarten und sammeln dabei viele Informationen. Darunter sind auch viele Informationen in Form von Zahlen, wie Populationsgröße (Anzahl der Tiere im untersuchten Gebiet), Nachkommen pro Jahr und Gestorbene pro Jahr. Aus diesen Informationen kann eine Formel erstellt werden, welche die Entwicklung der Populationsgröße beschreibt und Vorhersagen für die Zukunft ermöglicht. Für eine Vorhersage wird die aktuelle Populationsgröße in die Formel eingesetzt und nach der Berechnung erhält man die Anzahl der Tiere in einem Jahr. Und jetzt wird iteriert, also dieses Ergebnis erneut in die Formel eingesetzt um die Populationsgröße in zwei Jahren zu berechnen, und so weiter für die nächsten Jahre. Man erhält eine Zahlenfolge welche die Populationsgröße im Verlauf der nächsten Jahre darstellt.
Angenommen Naturschützer möchten eine bestimmte Tierart, beispielsweise Luchse, in einem bestimmten Gebiet, beispielsweise dem Harz, wieder ansiedeln. Dann müssen sie wissen wie viele Paare Luchse sie mindestens aussetzen müssen. Schließlich sollen die Luchse nicht wieder aussterben, sondern dauerhaft überleben. Also nehmen die Naturschützer die Formel mit der man die Entwicklung der Luchspopulation berechnen kann, setzen als Startpopulation beispielsweise 10 Paar ein und berechnen wie viele Tiere nach einem Jahr leben werden. Das Ergebnis dieser Berechnung wird wieder als Startpopulation in die Formel eingesetzt für die Berechnung des folgenden Jahres. Diese Berechnung wird für viele Jahre wiederholt, bis mit gewisser Sicherheit erkennbar ist, wie sich die Population entwickelt. Falls die Population gegen 0 geht, also ausstirbt, muss eine größere Anzahl von Paaren als Startpopulation gewählt und die Berechnung wiederholt werden. Das Einsetzen des Ergebnisses der vorherigen Berechnung als Startpopulation für die Berechnung des nächsten Jahres nennt der Mathematiker Iteration. Diese Vorgehensweise ist charakteristisch für die Berechnung von Fraktalen.
Die von den Zoologen gesammelten Informationen können fehlerhaft sein, man kann sich bei der Zählung der Jungtiere verzählt haben oder einen Todesfall nicht bemerkt haben. Deshalb können auch die Faktoren für Geburtenrate und Sterberate in der Formel zur Berechnung der Luchspopulation fehlerhaft sein. Deshalb müssen solche Berechnungen immer auch mit leicht abweichenden Werten für Geburtenrate und Sterberate wiederholt werden. Daraus ergibt sich eine sehr große Anzahl von Berechnungen und es entsteht schnell eine unübersichtliche Fülle von Zahlen. Um diese Berechnungen zu umgehen, wurden Möglichkeiten der grafischen Darstellung von Eigenschaften fraktaler Funktionen entwickelt. Dann sind nur die Berechnungen zur Erstellung der Grafik erforderlich. Anschließend kann man auf diesen Grafiken erkennen wie sich die Tierpopulationen entwickeln, abhängig von gewählten Werten für Startpopulation, Geburten- und Sterberate, ohne komplizierte Berechnungen ausführen zu müssen.
Eine von Mathematikern entwickelte Darstellung (weder beschreibt die Formel eine für Biologen wichtige Entwicklung, noch ist die dargestellte Eigenschaft für Biologen von Bedeutung) führte zu folgender Grafik:
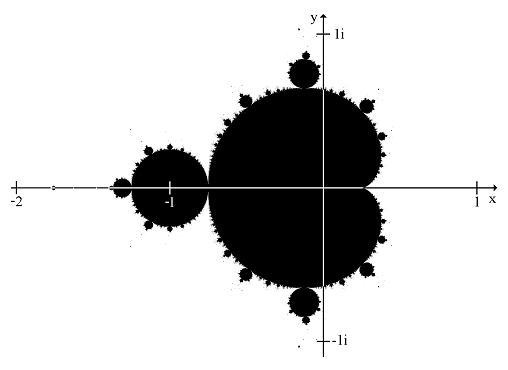
Mandelbrotmenge
1978 wurde erstmals mit einem Computer diese Grafik berechnet. Nach dem bedeutendsten Mathematiker auf dem Gebiet der Fraktale Benoit Mandelbrot, wird diese Grafik als Mandelbrotmenge bezeichnet. Umgangssprachlich hat sich allerdings die Bezeichnung „Apfelmännchen“ durchgesetzt.
Zurück zur Luchspopulation: Die Berechnung mit bestimmten Werten für Geburtenrate und Sterberrate kann ergeben, dass die Luchspopulation nach 10 Jahren deutlich abgenommen hat, aber noch existiert. Aber nach 20 Jahren ist die Luchspopulation ausgestorben. Aus der Abnahme kann man aber nicht schlussfolgern, dass die Luchspopulation aussterben wird. Möglich ist auch, dass nach einer Phase der Abnahme eine Erholung erfolgt. Es ist also die Berechnung für viele Jahre in der Zukunft, also eine große Zahl von Iterationen notwendig zur Klärung ob eine bestimmte Eigenschaft (Aussterben oder Überleben) erfüllt ist.
Also führt auch bei der Mandelbrotmenge eine größere Zahl an Iterationen zu einem genaueren Ergebnis.
Der Einfluss der Iteration, also das Einsetzen des Ergebnisses der vorherigen Berechnung als Startwert für die nächste Berechnung, zeigt folgende Abbildung:
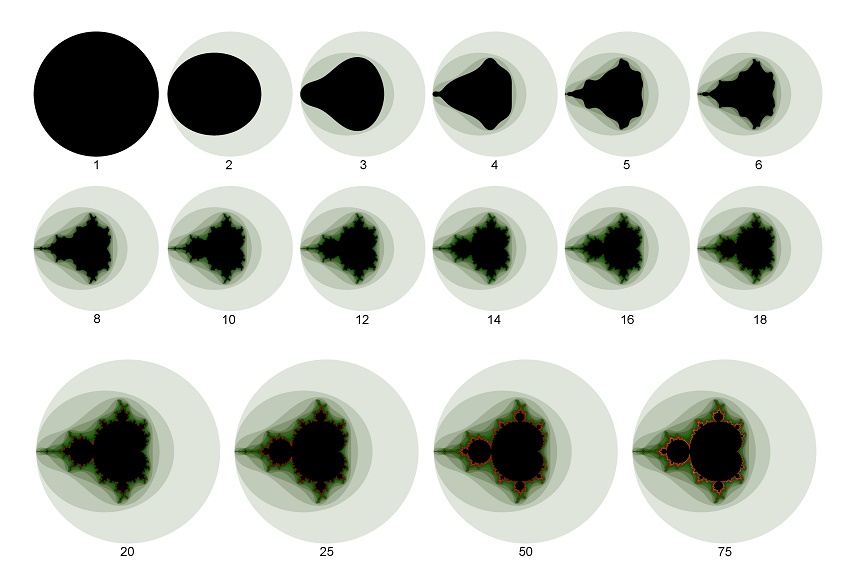
Iterationen 1-75
Jeder Iteration ist eine andere Farbe zugeordnet. Mit steigender Anzahl von Iterationen wird das Apfelmännchen kleiner, gleichzeitig bekommt der Rand eine immer komplexere Form.
Nach den ersten farbigen Berechnungen Anfang der 1980er wuchs die Neugier, wie genau der Rand des Apfelmännchens geformt ist, und so wurden einzelne Ausschnitte des Randes berechnet. Die folgende Abbildung zeigt wie der kleine, in umgekehrten Farben dargestellte Bereich, vergrößert aussieht. Die nächste Zeile der Abbildung zeigt den gleichen Ausschnitt wie zuvor, aber die Zahl der Iterationen wurde erhöht. Wieder wird der schwarze Bereich des Apfelmännchen kleiner und der Rand bekommt eine komplexere Form. Der kleine, in umgekehrten Farben dargestellte Bereich ist daneben vergrößert dargestellt.
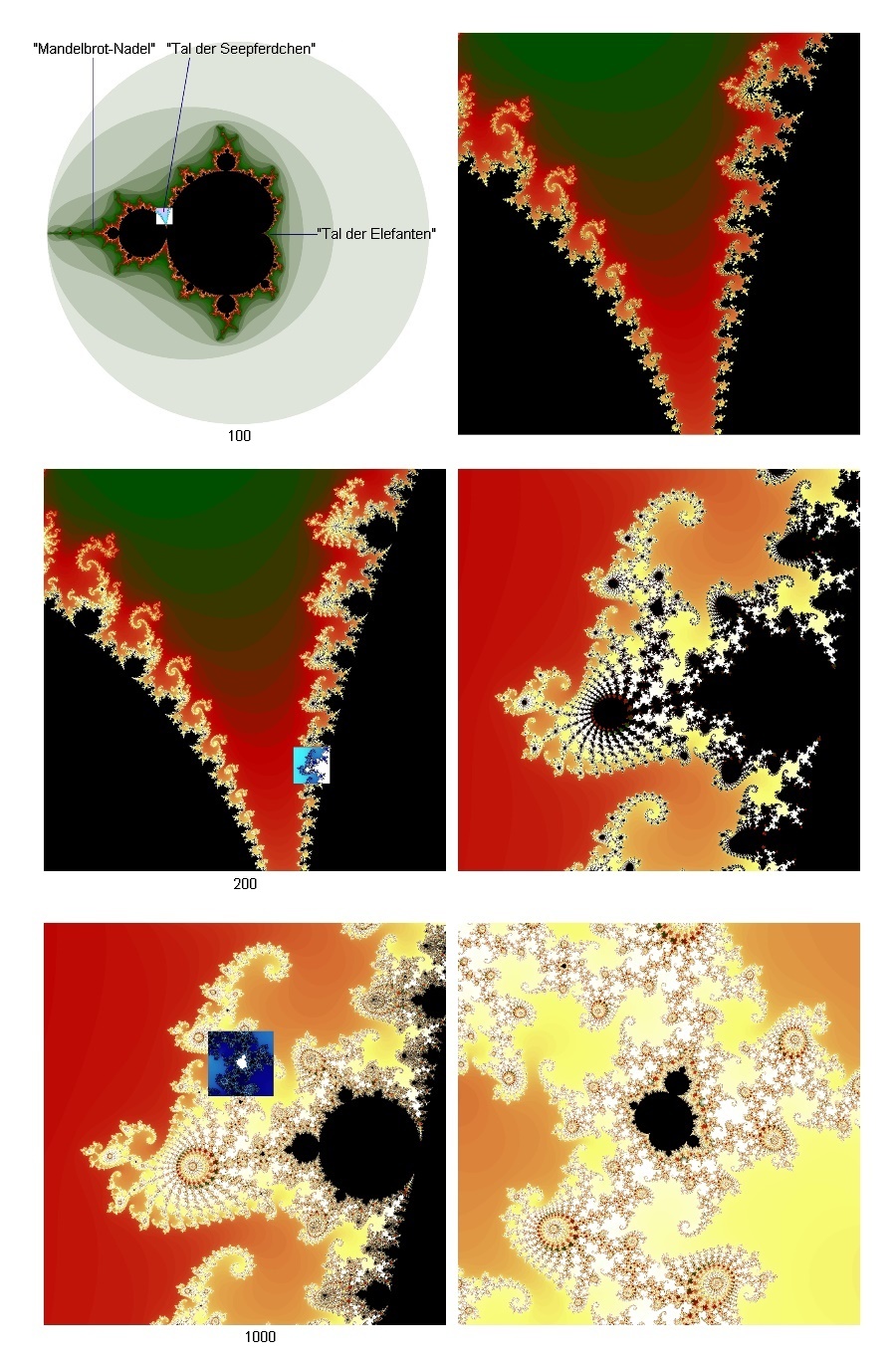
Iterationen 100-1000
Es zeigte sich, dass der Rand komplexe Formen aufweist, die einen gewissen ästhetischen Reiz haben. Obwohl niemand die Absicht hatte etwas zu erschaffen, das schön aussieht, ist es einfach passiert. Seit den 1980 Jahren wurden deshalb zahlreiche Programme geschrieben, deren einziger Zweck es ist, diese schönen Bilder zu erzeugen. Damalige Computer benötigten für solche Berechnungen noch mehrere Stunden, manchmal sogar mehrere Tage. Heutige Computer benötigen für Bilder wie in der Abbildung "Iteration 100-1000" nur wenige Sekunden. Die Farben sind frei wählbar und durch Filter können die Farbverteilung verändert werden, fließende Farbverläufe, Wellen, Stacheln und ähnliches erzeugt werden.

Verschiedene Formeln
2009 entwickelten die Mathematiker Daniel White und Paul Nylander eine Möglichkeit 3D-Fraktale zu berechnen. Auch 3D-Fraktale haben einen ästhetischen Reiz. Durch verschiedene Effekte wie Licht und Schatten, Schärfentiefe, Atmosphäre, Nebel usw. entstehen Bilder, die wie Fotos von mikroskopisch kleinen Objekten, exotischen Landschaften oder futuristischen Bauwerken wirken.
Weiter mit:
Fraktale Natur
Fraktal-Programme